Πριν από την ημερομηνία διεξαγωγής του φετινού Πανελλήνιου Διαγωνισμού Λύσης Σκακιστικών Προβλημάτων (Κυριακή 01/06/2008), παρουσιάζουμε τα προβλήματα που δόθηκαν στον περυσινό διαγωνισμό. Ο στόχος είναι να εξοικειωθούν με τα ζητούμενα οι επίδοξοι λύτες.
Είναι σημαντικό να συμμετέχουμε. Η εξάσκηση σε πραγματικές συνθήκες βελτιώνει τον λύτη.
Ας παρατηρήσουμε μέσα στις λύσεις τον τρόπο βαθμολόγησης, το πώς κατανέμονται οι βαθμοί στις διάφορες βαριάντες. Οι βαθμοί αναγράφονται μέσα σε αγκύλες με έντονα στοιχεία. Δεν πρέπει να παραλείπουμε σημαντικές βαριάντες.
6ος ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΛΥΣΗΣ ΣΚΑΚΙΣΤΙΚΩΝ ΠΡΟΒΛΗΜΑΤΩΝ
Οργάνωση : Ελληνική Σκακιστική Ομοσπονδία, Σ.Ο. Αιγάλεω και Δήμος Αιγάλεω
Ημερομηνία : 03 Ιουνίου 2007
Ελεγκτής : Χάρης Φουγιαξής
Οδηγίες : Η σωστή και πλήρης λύση κάθε προβλήματος βαθμολογείται με 5 βαθμούς. Η μη πλήρης λύση βαθμολογείται με λιγότερους βαθμούς.
#2 : Γράψτε μόνο την πρώτη κίνηση (το "κλειδί").
#3 : Γράψτε το κλειδί, την απειλή (αν υπάρχει) και όλες τις βαριάντες μέχρι και τη 2η κίνηση των λευκών.
Πολυκίνητο : Γράψτε το κλειδί, την απειλή (αν υπάρχει) και όλες τις βαριάντες μέχρι και την προτελευταία κίνηση των λευκών.
Σπουδή: Γράψτε όλες τις κινήσεις μέχρι τη θέση προφανούς νίκης των λευκών.
Αντίστροφο : Γράψτε το κλειδί, την απειλή (αν υπάρχει) και όλες τις βαριάντες μέχρι και την τελευταία κίνηση των λευκών.
Βοηθητικό : Γράψτε όλες τις κινήσεις (για όλες τις λύσεις). Τα μαύρα παίζουν πρώτα.
1ος ΓΥΡΟΣ, Χρόνος : 2 ώρες
 | (Πρόβλημα 169) Touw Hian Bwee, Τέταρτο Βραβείο 113th TT British Chess Federation, 1966-67 Ματ σε 2 κινήσεις. #2 (8+11) |
| [b3R2r/p4sB1/3kSR2/1Q1p1B2/7q/3sP2p/5p2/b4K2] | |
Υπάρχουν μερικές δοκιμές : {1.Sd4+? Qxf6!}, {1.Sg5+? Bxf6!}, {1.Qd7+? Kxd7!}, {1.Qb8+? Kc6!}, {1.Qb6+? axb6!}, {1.Qc5+? Sxc5!}. Η λύση ακολουθεί :
Κλειδί : 1.Qa5! [5.0] ( > 2.Qc7#)
1...Kd7 2.Sc7#, 1...Kc6 2.Sd8#, 1...Ke5 2.Sf8#, 1...Qc4 2.Sd4#, 1...d4 2.Sg5#
 | (Πρόβλημα 170) M. Marandyuk & V. Melnichenko, Τέταρτο Βραβείο S. Brehmer MT, Die Schwalbe 1996-98 Ματ σε 3 κινήσεις. #3 (9+8) |
| [8/3BBbp1/p4b2/1P1kP3/1P2R1s1/1K1Pp3/2S3s1/8] | |
Αν κινηθεί ο μαύρος Βασιλιάς, ο λευκός Βασιλιάς θα απειληθεί με σαχ από τον μαύρο Αξιωματικό Bf7.
Υπάρχουν μερικές δοκιμές : {1.Bd6? Bxe5!}, {1.Kb2? Bxe5+!}, {1.Bc6+? Ke6!}, {1.exf6? axb5!}, {1.Rd4+? Kxe5+!}, {1.Sd4? Sxe5!}. Η λύση ακολουθεί :
Κλειδί : 1.Ka3! [1.0] ( > 2.Rd4+ [1.0] Kxe5 3.Bd6#)
1...Bxe5 2.Sd4 [1.0] ( > 3.Bc6#) Be8 3.Be6#
1...Bg5 / Bh4 2.Bd6 [1.0] ( > 3.Rd4#)
1...Bxe7 2.Bc6+ [1.0] Ke6 3.Sd4#
 | (Πρόβλημα 171) Michael Herzberg, Δεύτερο Βραβείο Problem-Forum 2000 Ματ σε 5 κινήσεις. #5 (7+7) |
| [8/1B3p2/4r1p1/2pS4/P1k2p2/5S1K/1pPB4/8] | |
Δοκιμές : {1.Sc7? Rd6!}, {1.Sb6+? Rxb6!}, {1.Ba5? ( > 2.Sd2+ Kd4 3.Bc3#) b1=S!}. Ακολουθεί η λύση :
Κλειδί : 1.Sxf4! [1.0] ( > 2.Bd5#)
1...Rd6 2.Sd5! [1.0] ( > 3.Se3#)
2...Re6 3.Ba5! [1.0] ( > 4.Sd2+ [1.0] Kd4 5.Bc3#)
3...b1=S 4.Bc6 [1.0] ( > 5.Sb6#)
4...Rxc6 5.Se3# (Το ματ γίνεται από τετράγωνο που ήταν διπλά προστατευμένο).
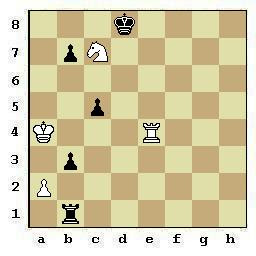 | (Πρόβλημα 172) Nikolay Kralin & Leonid Sokolenko, Πρώτο Βραβείο Thèmes-64, 1983 Παίζουν τα Λευκά και νικούν. + (4+5) |
| [3k4/1pS5/8/2p5/K3R3/1p6/P7/1r6] | |
Κλειδί : 1.Se6+ (απειλεί το πιόνι της στήλης-c) Kc8
2.axb3 b5+
3.Ka3 c4 (προστατεύεται το πιόνι της στήλης-c)
4.b4 [1.0] Rb3+ (βρίσκει ευκαιρία να πάρει το λευκό πιόνι)
5.Ka2 Rxb4 (αλλά ο μαύρος Πύργος έχει μικρή κινητικότητα)
6.Sc5! [1.5] Kd8 (δεν μπορεί να βγεί από το c7 λόγω του Sa6+ και χάνεται ο μαύρος Πύργος)
7.Ka1! [1.5] Kc8 (και τώρα θα περιοριστεί και ο μαύρος Βασιλιάς)
8.Rd4 [1.0] Kc7 / Kb8
9.Sa6+ +-
 | (Πρόβλημα 173) Frank Richter, Πρώτη Εύφημη Μνεία Schach 1984 Αντίστροφο σε 3 κινήσεις s#3 (9+7) |
| [5S2/1p5b/2P5/1Qbk1P2/P2s4/7p/6pB/1B1R2K1] | |
Φαίνεται ότι, αν απομακρυνθεί η Βασίλισσα και αναγκάσουμε τον μαύρο Ίππο να κινηθεί, το ματ από τον μαύρο Αξιωματικό Bc5 είναι πιθανό.
Δοκιμές : {1 Qb3+? Kxc6!}, {1 Qxc5+? Kxc5!}, {1 Rxd4+? Kxd4!}, {1 Be4+? Kxe4!}, {1 Ba2+? Ke4!}.
Κλειδί : 1.c7! [1.0] ( > 2.Qxb7+ Kc4 3.Rc1+ [1.0] Sc2#)
1...Bxf5 2.Ba2+ Ke4 3.Qe2+ [1.5] Sxe2#
1...b6 2.Qb3+ Kc6 3.Qf3+ [1.5] Sxf3#
1.Kc5+ Rd3 2.Qxc6 Rd6 3.Bd4 Rxc6#
1.Kc4+ Sd5 2.Sbd4 Sxc7 3.Rb4 Rxc3#
1.Ke4+ Bd2 2.Sfd4 Bxg5 3.f5 Re3#
Μία λύση = [2.0], δύο λύσεις = [4.0], τρεις λύσεις = [5.0]
2ος ΓΥΡΟΣ, Χρόνος : 2 ώρες
 | (Πρόβλημα 175) Erich Brunner, Πρώτο Βραβείο Leipziger Tageblatt 1924 Ματ σε 2 κινήσεις. #2 (10+9) |
| [K1B4b/p6q/P3R2r/r3k4/6p1/B1p1Q1Ps/1R1SS3/8] | |
Το πρόβλημα είναι πλήρους αποκλεισμού (complete block). Όποια κίνηση και να παίξουν τα μαύρα από τις 34 διαθέσιμες, υπάρχει έτοιμο ματ. Για παράδειγμα, 1...Qb1 2.Bb7#].
Από τις 21 δοκιμές αναφέρουμε μία : {1.Rb8? (zz) Qb1!}.
Κλειδί : 1.Rb7! [5.0] (zz)
Βαριάντες :
1...Q~b1 (οπουδήποτε προς το b1) / Bg7 2.Rd7#,
1...Q~7 (οπουδήποτε στην γραμμή-7) / Qe4 / Rg6 2.Q(x)e4#,
1...Qxb7+ 2.Bxb7#, 1...S~ 2.Sf4#, 1...Rxe6 2.Qxe6#, 1...Rh4 / Bf6 2.Rd6#,
1...Bd4 2.Qxd4#, 1...Be5 2.Qxe5#, 1...c~ 2.Qb3#, 1...Rc5 2.Qxc5#, 1...Rb5 / Rxa3 2.R(x)b5#.
 | (Πρόβλημα 176) Mikhail Kuznetsov, Πρώτο Βραβείο ‘64’ 1985 Ματ σε 3 κινήσεις. #3 (9+8) |
| [6K1/3S2S1/4R1p1/s2kp3/BR3pP1/7Q/q1P1b3/3s4] | |
Δοκιμές : {1 Se8? Qc4!}, {1 Sb6+? / Sf6+? Kc5!}, {1 Rxe5+? / Rd6+? K(x)d6+!}, {1 Bc6+? Sxc6!}, {1 Qg2+? / Qh1+? f3!}, {1 Qf3+? Bxf3!}, {1 Qd3+? Bxd3!}, {1 Qc3? Sxc3!}, {1 Qb3+ Qxb3!}.
Η λευκή Βασίλισσα δημιουργεί μπαταρία πλαγιοκόπησης (indirect battery) με τον Πύργο Rb4. Αυτή δεν είναι άμεση μπαταρία, επειδή δεν σημαδεύει τον μαύρο Βασιλιά αλλά διαφυγές του. Ο μαύρος θα προσπαθήσει να βάλει κάτι στο c4 για να δημιουργήσει διαφυγή στο d4. Αν η μαύρη Βασίλισσα εγκαταλείψει την διαγώνιο a2-g8, ο λευκός Βασιλιάς δεν απειλείται με πιθανό σαχ από αποκάλυψη και μπορεί να το εκμεταλλευτεί.
Κλειδί : 1.Qa3! [0.5] ( > 2.Sb6+ [0.5] Kc5 3.Rc4#)
1...Qc4 2.Rxe5+ [1.0] Kd6+ / Kd4+ 3.Rxc4# / Se6#
1...Bc4 2.Qf3+ [1.0] Kd4 / e4 3.Qd3# / Qxe4#
1...Sc4 2.Bc6+ [1.0] Kd4 3.Rd6#
1...Qxa3 2.Rxe5+ [1.0] Kd6 3.Se8#
 | (Πρόβλημα 177) Angel Zlatanov, Τέταρτη Εύφημη Μνεία Zadachi i Etyudy, 2000 Ματ σε 4 κινήσεις. #4 (4+9) |
| [6r1/p3Q1p1/K1k3S1/2S3p1/82p5/4pp2/3s4/] | |
Δοκιμές : {1.Qd6+? Kxd6!}, {1 Qe4+? / Qe6+? / Qd7+? Kxc5!}, {1 Qe5? Re8!}, {1 Se5+? / Se4? / Sb7? Kd5!}.
Κλειδί : 1.Se6! [0.5] ( > 2.Qc5+ Kd7 3.Qd5+ [1.5] Kc8 / Ke8 4.Qb7# / Sc7#)
1...Se3 2.Qc7+ Kd5 3.Qd7+ [1.5] Kc4 / Ke4 4.Qb5# / Sxg5#
1...Kd5 2.Qd7+ Ke4 3.Sc5+ [1.5] Ke3 / Kf3 4.Qd3# / Qh3#
 | (Πρόβλημα 178) Dmitry Petrov, Vecherny Novosibirsk 1979 Παίζουν τα Λευκά και νικούν. + (6+7) |
| [5b1q/7p/4P1Rp/1B4pk/3P4/4p1K1/8/1R6] | |
Κλειδί : 1.e7! Bxe7 (Δεν αφήνει να προαχθεί το πιόνι. Όχι [1...Qxd4 2.Rxh6+ και exf8=Q+ / Be8+])
2.Bd3 [1.5] Qxd4
3.Rh1+ Qh4+ (απαλλάσσεται από την μαύρη Βασίλισσα ...)
4.Rxh4+ gxh4+ (... και στριμώχνει τον μαύρο Βασιλιά)
5.Kf4 Bg5+
6.Kf3 [2.0] hxg6
7.Be2 [1.5] +-
 | (Πρόβλημα 179) Vukota Nikoletic, Βραβείο Mat Plus 1995 Αντίστροφο σε 3 κινήσεις. S#3 (9+9) |
| [8/1r2SR1p/3B3P/4rBSK/5k2/2p2pq1/2p1R2Q/7b] | |
Κλειδί : 1. Re1! [1.0] ( > 2.Qd2+ cxd2 3.Sh3+ [1.0] Qxh3#)
1...Qxh2+ 2.Bh3+ Kg3 3.Rxf3+ [1.0] Bxf3#
1...Bg2 2.Sh3+ Bxh3 3.Sg6+ [1.0] hxg6#
1...f2 2.Sd5+ Bxd5 3.Bd7+ [1.0] Bxf7#
 | (Πρόβλημα 180) Chris Feather, Shakhmatna Misl 2005 Βοηθητικό σε 4 κινήσεις. (2 λύσεις). h#4 2.1.1.1. (3+9) |
| [3k4/1pS5/8/2p5/K3R3/1p6/P7/1r6] | |
Κλειδί : 1.Rg8! Re6 2.Rg7 fxg7 3.Bc6 g8=Q 4.Bb5 Qa8# [2.5]
Κλειδί : 1.Re4! Re7 2.Rxe7 fxe7 3.Ra8 e8=S 4.Ra7 Sc7# [2.5]






















